Archimedean Spiral

Back to the prime numbers playground. I recently bumped once again on the odds of shapes and other interesting facts about prime numbers. However, this time is about a noticeable gap on the Archimedean Spiral. Note these are, I believe, classical number theory chapters, but for me is interesting to work on some codes and check myself, so there it goes.

Imagine you have a sequence of integers. The simplest sequence ever, so 1, 2, 3, 4 ... Then you decided to plot these numbers using polar coordinates where x is equal y (in radians). While y measure the angle in radian, x measures the radius or distance from (0,0). You would get something like this:

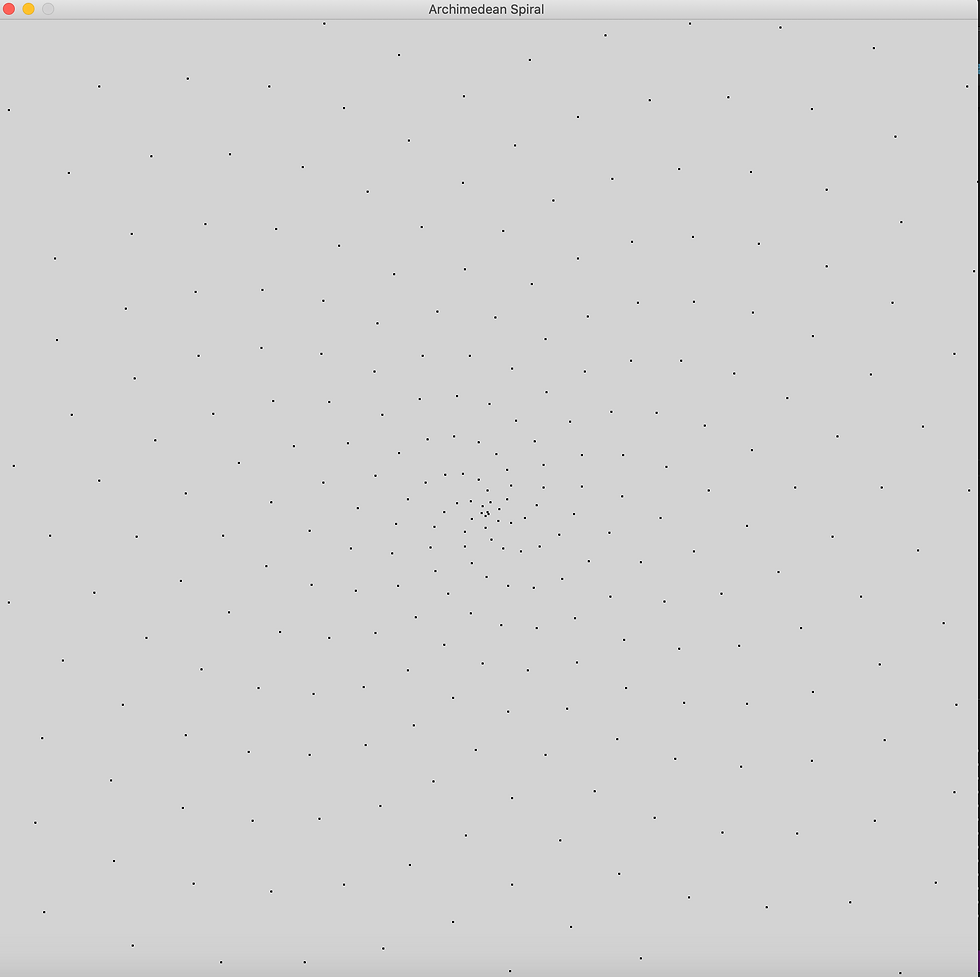
Plotting few the dots from the sequence you results on the next figure.

It is noticeable few dots here and there. Zooming out and using a larger sequence, you then have a better picture of a spiral.

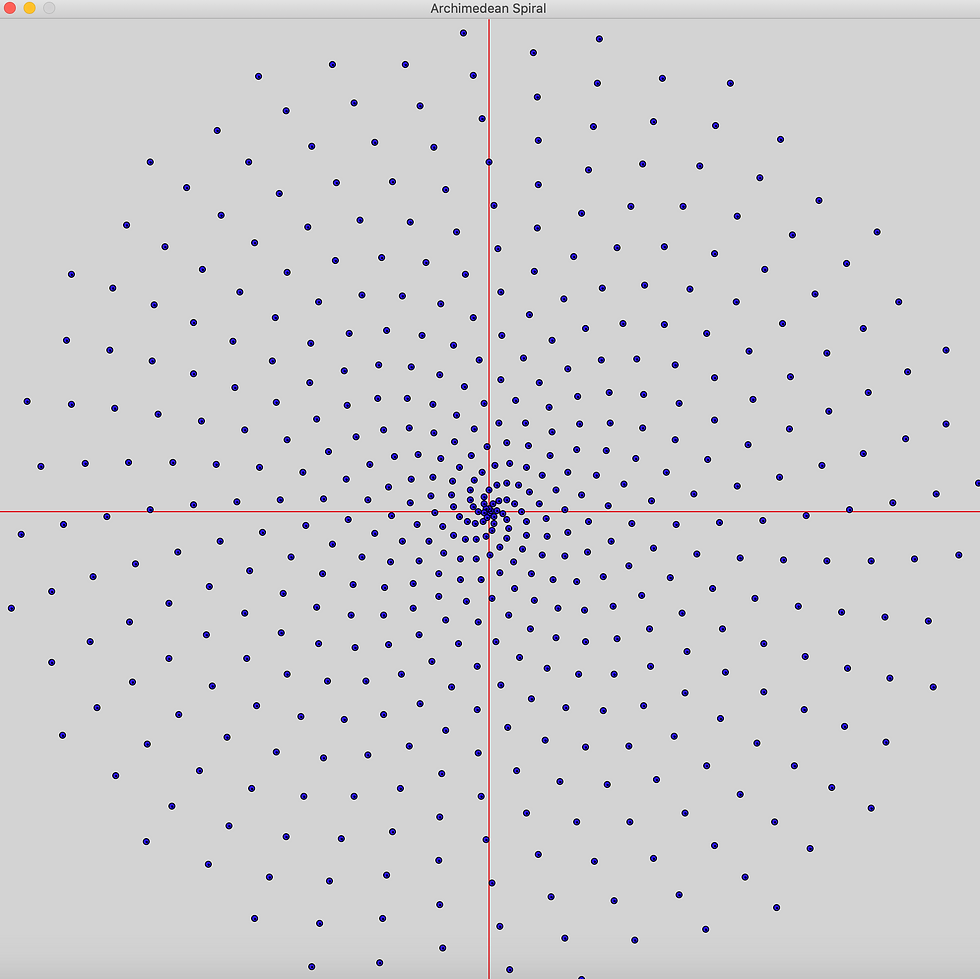
This gets a little more interesting. We can see the spiral shape with 6 arms. There's a reason why we count 6. This is related to the measure of a circle, or a full turn, in radians, which is 2*pi, approximately 6.28 rads. for every 6 plotted dots it starts a new round slightly shifted. This is what forms the spiral shape.

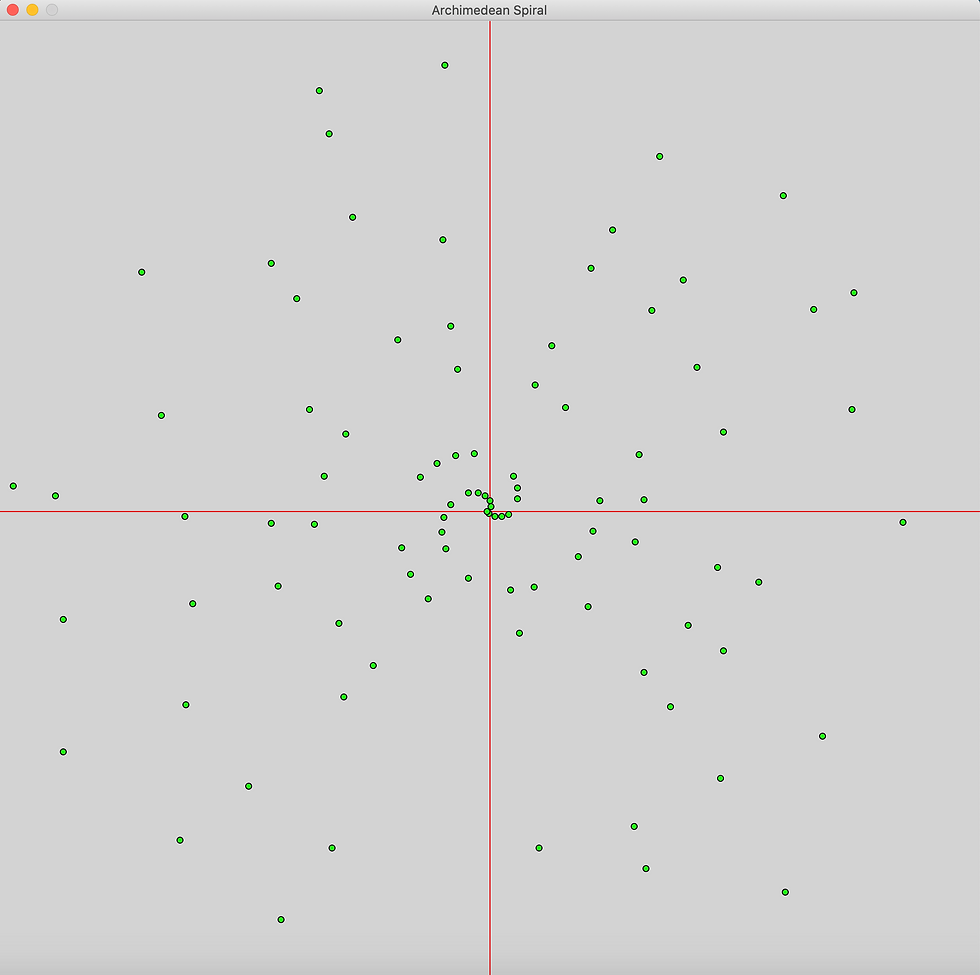
The Archimedean Spiral is the exact same spiral but filtering out all the non prime numbers. Doing it on the same scale as the figure above, we'd get the following image:

Filtering the numbers and displaying the primes only we get:

We can see a spiral shape forming here. But this plot has only few points. What happens if we filter the primes on a sequence of 10000 numbers and zoom it out? This is what we get.

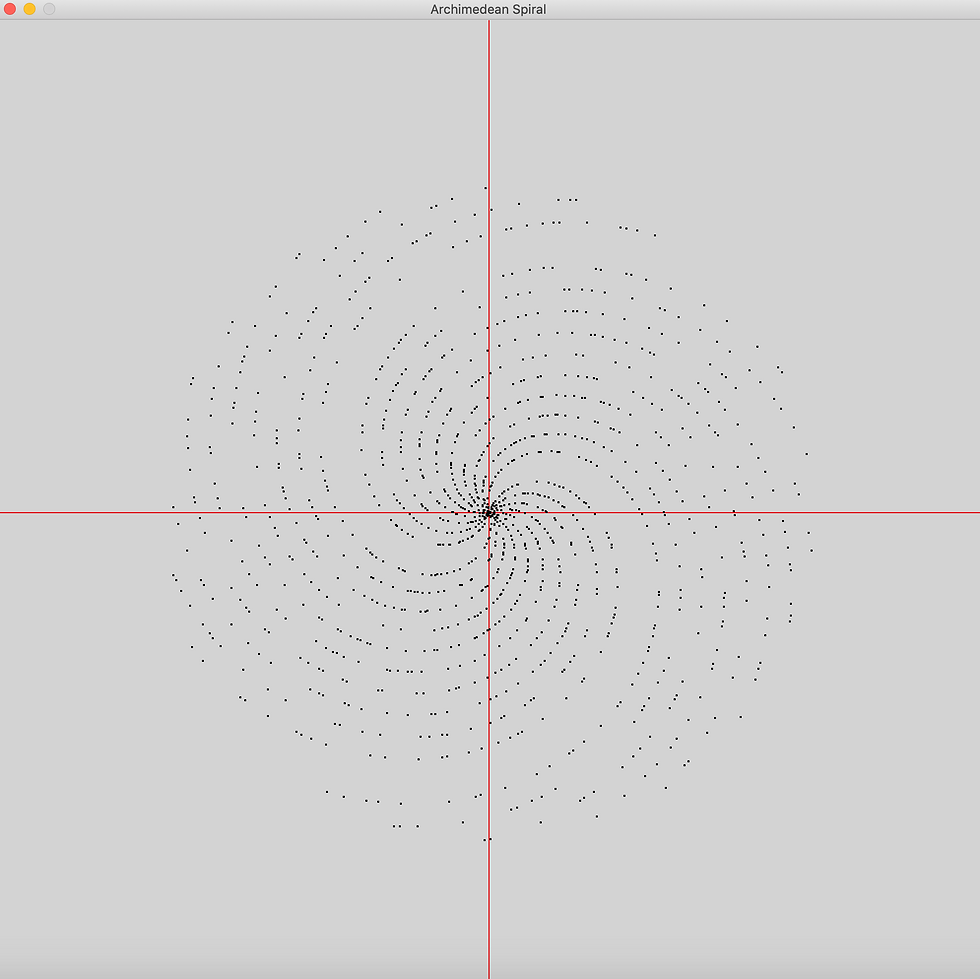
We start noticing few larger gaps between arms on this spiral. Those gaps are intervals where we can't find prime numbers. Plotting 100000 dots, it became a lot more evident.

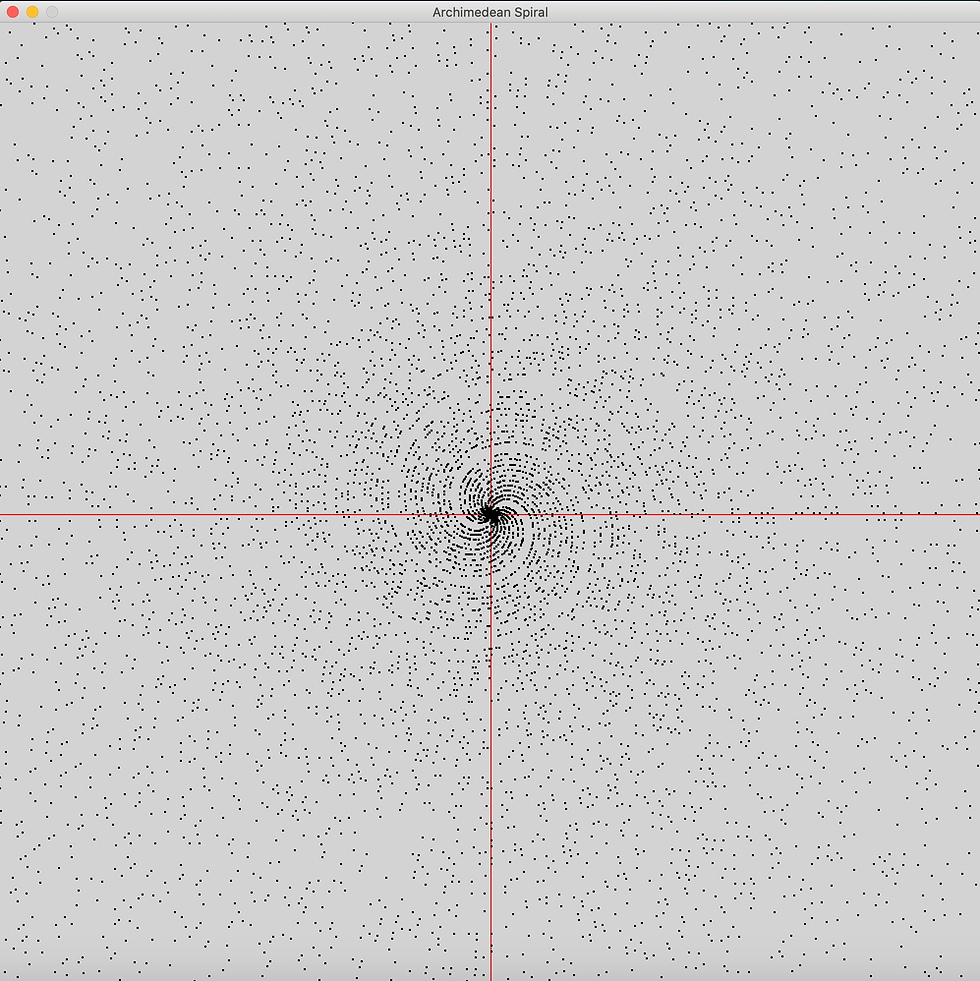
Looking carefully it is noticeable gaps with no dots formed by the archemedian spiral.

So, for this little program, I've implemented a Sieve of Erasthotenes that filter all the primes on the 150000 numbers. I even ran this for 1 million numbers and runs pretty fast. The time complexity for this algorithm is O(nlog logn). My routine returns an array of boolean that forces me to create another array with primes only. It's not the best space optimization, but works fine in terms of time complexity (O(n)). It's fun to see an algorithm developed on ancient Greece (BC) working on modern computers. The idea is very basic and suits this problem very well.